The 80-20 rule or Pareto principle states that, often in life, 20% of effort can roughly achieve 80% of the desired effects. An interesting question is as to weather this rule also holds in the context of information acquisition from redundant data that follows a power law frequency distribution. Can we learn 80% of URLs on the Web by parsing only 20% of the web pages? Can we learn 80% of the used vocabulary by looking at only 20% of the tags? Can we learn 80% of the news by reading 20% of the newspapers? More generally, can we learn 80% of all available information in a corpus by randomly sampling 20% of data (without replacement)?
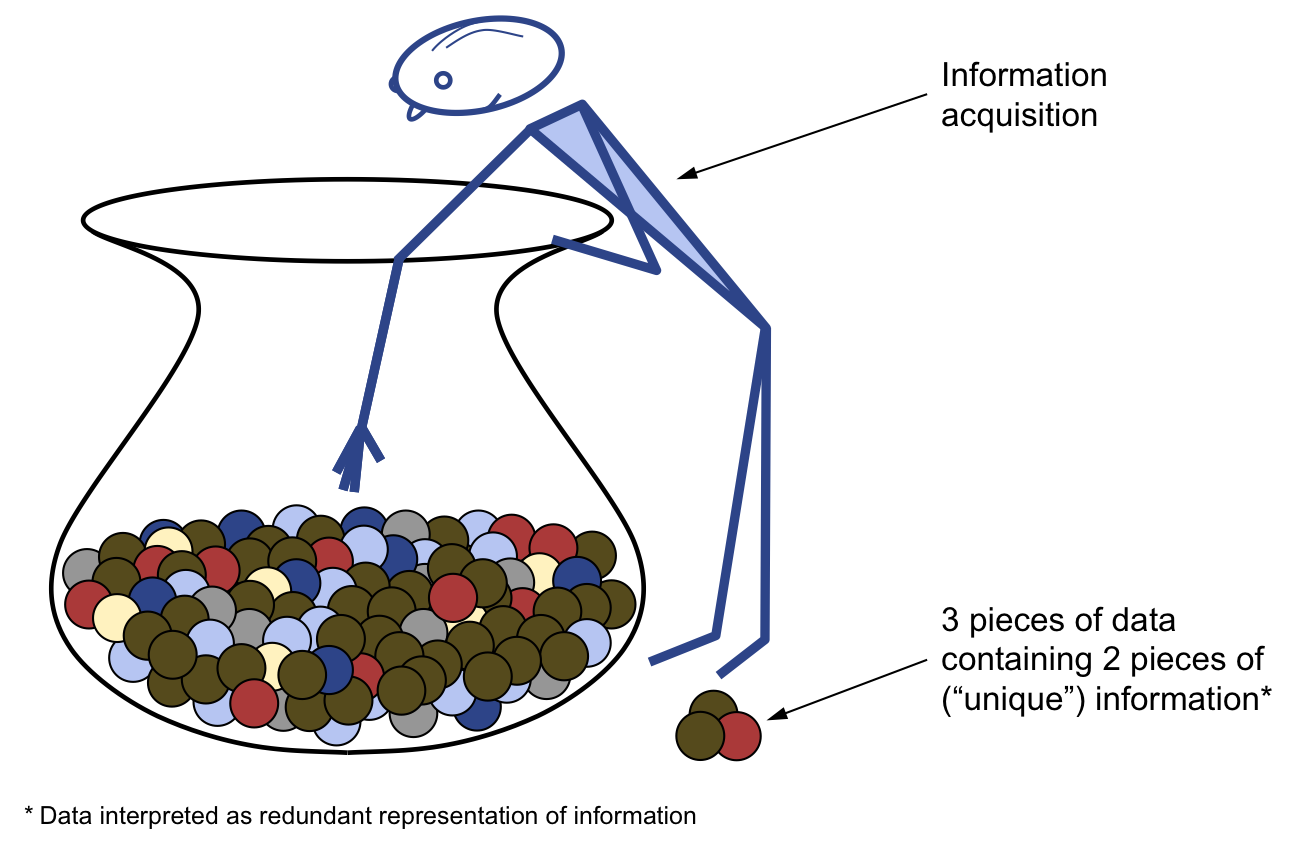
Information Acquisition from redundant Data
We develop an abstract model of information acquisition from redundant data: We assume a random sampling process without replacement from an infinitely large data set which contains information with bias. We are then interested in the fraction of total information we can expect to learn as function of (i) the sampled fraction (our "recall") and (ii) the bias of information (its "redundancy distribution").
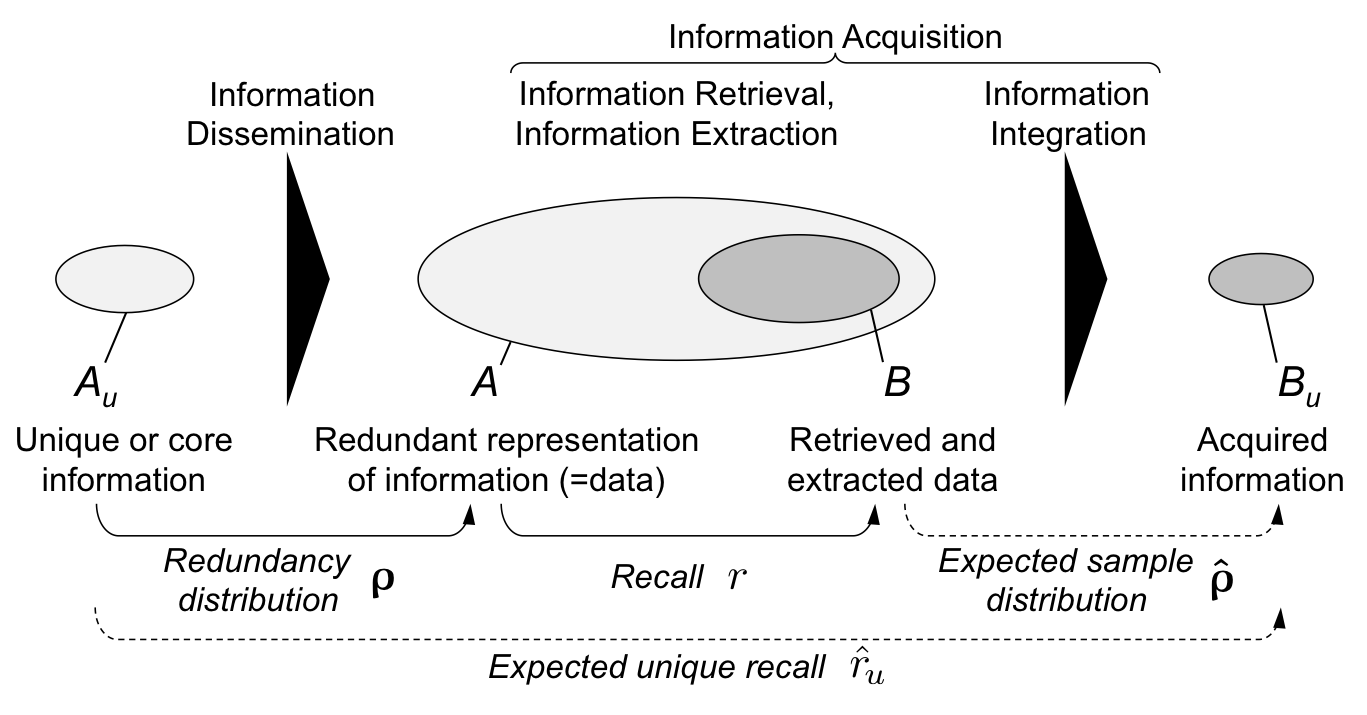
We develop two rules of thumb with varying robustness. We first show that, when information bias follows a Zipf distribution, the 80-20 rule or Pareto principle does surprisingly not hold, and we can rather expect to learn less than 40% of the information when randomly sampling 20% of the overall data. We then analytically prove that for large data sets, randomized sampling from power-law distributions leads to "truncated distributions" with the same power-law exponent. This second rule is very robust and also holds for distributions that deviate substantially from a strict power law. We further give one particular family of power-law functions that remain completely invariant under sampling.
Publications
- Rules of Thumb for Information Acquisition from Large and Redundant Data
Wolfgang Gatterbauer
ECIR 2011, pp. 479-490.
[Paper], [Presentation], [Presentation], [bib]
Full 40 page version with all proofs (arXiv:1012.3502 [cs.IR]): [Full version], [bib], (Version Dec 2010)
-
Estimating Required Recall for Successful Knowledge Acquisition from the Web
Wolfgang Gatterbauer.
WWW 2006, pp. 969-970 (Poster Paper).
[Paper], [Poster], [Poster1+2], [bib]
People
| (Associate Professor @ NEU) |
Funding
This research is motivated by the VENTEX (Visualized Element Nodes Table EXtraction) project and was supported in part by a DOC scholarship from the Austrian Academy of Sciences, by the FIT-IT program of the Austrian Federal Ministry for Transport, Innovation and Technology, and NSF grant IIS-0915054 (the BeliefDB project). Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author(s) and do not necessarily reflect the views of the National Science Foundation or other agencies.